Η ράβδος ΟΒ είναι ομογενής έχει βάρος 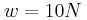 και έχει μήκος
και έχει μήκος 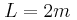 . Το ένα άκρο της Ο στηρίζεται σε τοίχο με άρθρωση, ενώ στο άλλο έχουμε δέσει νήμα το οποίο σχηματίζει γωνία
. Το ένα άκρο της Ο στηρίζεται σε τοίχο με άρθρωση, ενώ στο άλλο έχουμε δέσει νήμα το οποίο σχηματίζει γωνία 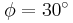 με το οριζόντιο επίπεδο. Πάνω στη ράβδο βρίσκεται οριζόντιο ελατήριο σταθεράς
με το οριζόντιο επίπεδο. Πάνω στη ράβδο βρίσκεται οριζόντιο ελατήριο σταθεράς 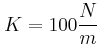 που στο ένα άκρο του έχουμε δέσει σώμα μάζας
που στο ένα άκρο του έχουμε δέσει σώμα μάζας 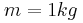 που ισορροπεί ακίνητο. Το φυσικό μήκος του ελατηρίου είναι
που ισορροπεί ακίνητο. Το φυσικό μήκος του ελατηρίου είναι 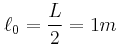 . Τη χρονική στιγμή
. Τη χρονική στιγμή 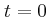 εκτοξεύεται το σώμα με ταχύτητα
εκτοξεύεται το σώμα με ταχύτητα 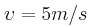 προς τα δεξιά ,οπότε το σώμα ξεκινάει να εκτελεί γραμμική αρμονική ταλάντωση. (Υπόδειξη: Ως θετική φορά θεωρείστε τη κατεύθυνση προς τα δεξιά.)
προς τα δεξιά ,οπότε το σώμα ξεκινάει να εκτελεί γραμμική αρμονική ταλάντωση. (Υπόδειξη: Ως θετική φορά θεωρείστε τη κατεύθυνση προς τα δεξιά.)

Να βρεθεί:
α) Η τάση του νήματος πριν την εκτόξευση του σώματος.
β) Το πλάτος της ταλάντωσης του σώματος.
γ) Η τάση του νήματος τη χρονική στιγμή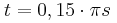 .
.
δ) Το μέτρο της δύναμης που δέχεται το σώμα από την άρθρωση τη χρονική στιγμή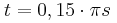 .
.
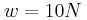 και έχει μήκος
και έχει μήκος 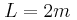 . Το ένα άκρο της Ο στηρίζεται σε τοίχο με άρθρωση, ενώ στο άλλο έχουμε δέσει νήμα το οποίο σχηματίζει γωνία
. Το ένα άκρο της Ο στηρίζεται σε τοίχο με άρθρωση, ενώ στο άλλο έχουμε δέσει νήμα το οποίο σχηματίζει γωνία 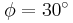 με το οριζόντιο επίπεδο. Πάνω στη ράβδο βρίσκεται οριζόντιο ελατήριο σταθεράς
με το οριζόντιο επίπεδο. Πάνω στη ράβδο βρίσκεται οριζόντιο ελατήριο σταθεράς 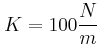 που στο ένα άκρο του έχουμε δέσει σώμα μάζας
που στο ένα άκρο του έχουμε δέσει σώμα μάζας 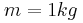 που ισορροπεί ακίνητο. Το φυσικό μήκος του ελατηρίου είναι
που ισορροπεί ακίνητο. Το φυσικό μήκος του ελατηρίου είναι 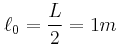 . Τη χρονική στιγμή
. Τη χρονική στιγμή 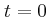 εκτοξεύεται το σώμα με ταχύτητα
εκτοξεύεται το σώμα με ταχύτητα 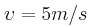 προς τα δεξιά ,οπότε το σώμα ξεκινάει να εκτελεί γραμμική αρμονική ταλάντωση. (Υπόδειξη: Ως θετική φορά θεωρείστε τη κατεύθυνση προς τα δεξιά.)
προς τα δεξιά ,οπότε το σώμα ξεκινάει να εκτελεί γραμμική αρμονική ταλάντωση. (Υπόδειξη: Ως θετική φορά θεωρείστε τη κατεύθυνση προς τα δεξιά.)
Να βρεθεί:
α) Η τάση του νήματος πριν την εκτόξευση του σώματος.
β) Το πλάτος της ταλάντωσης του σώματος.
γ) Η τάση του νήματος τη χρονική στιγμή
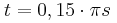 .
.δ) Το μέτρο της δύναμης που δέχεται το σώμα από την άρθρωση τη χρονική στιγμή
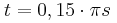 .
.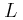 και βάρους
και βάρους 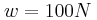 ισορροπεί όπως φαίνεται στο σχήμα στηριζόμενη στο άκρο της Α σε λείο τοίχο και στο άκρο της Β σε τραχύ έδαφος. Δίνεται ότι η ελάχιστη γωνία για την οποία η ράβδος δεν ολισθαίνει είναι
ισορροπεί όπως φαίνεται στο σχήμα στηριζόμενη στο άκρο της Α σε λείο τοίχο και στο άκρο της Β σε τραχύ έδαφος. Δίνεται ότι η ελάχιστη γωνία για την οποία η ράβδος δεν ολισθαίνει είναι 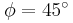 και ότι
και ότι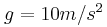 .
.
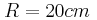 και μπορεί να περιστρέφεται γύρω από σταθερό άξονα χωρίς τριβές. Από το αυλάκι της τροχαλίας είναι δεμένο με αβαρές μη εκτατό νήμα ένα σώμα Σ. Αφήνουμε ελεύθερο το σώμα και αυτό κατεβαίνοντας αποκτά επιτάχυνση
και μπορεί να περιστρέφεται γύρω από σταθερό άξονα χωρίς τριβές. Από το αυλάκι της τροχαλίας είναι δεμένο με αβαρές μη εκτατό νήμα ένα σώμα Σ. Αφήνουμε ελεύθερο το σώμα και αυτό κατεβαίνοντας αποκτά επιτάχυνση 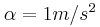 ενώ η τροχαλία εκτελεί στροφική κίνηση.
ενώ η τροχαλία εκτελεί στροφική κίνηση.
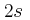 αφού αφήσουμε το σώμα ελεύθερο.
αφού αφήσουμε το σώμα ελεύθερο.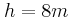 , πόσες στροφές θα έχει εκτελέσει η τροχαλία.
, πόσες στροφές θα έχει εκτελέσει η τροχαλία.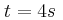 κόβουμε το νήμα και το σώμα πλέον πέφτει με επιτάχυνση
κόβουμε το νήμα και το σώμα πλέον πέφτει με επιτάχυνση 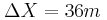 .
.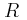
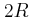
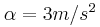

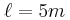
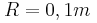
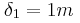 και
και 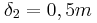 και αρχικά κινείται με ταχύτητα
και αρχικά κινείται με ταχύτητα 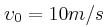 . Ο οδηγός πατάει φρένο για κάποιο λόγο και οι τροχοί αρχίζουν να επιβραδύνονται. Αν γνωρίζουμε ότι η επιτάχυνση του τρακτέρ είναι σταθερή και ίση με
. Ο οδηγός πατάει φρένο για κάποιο λόγο και οι τροχοί αρχίζουν να επιβραδύνονται. Αν γνωρίζουμε ότι η επιτάχυνση του τρακτέρ είναι σταθερή και ίση με 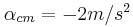 , να βρεθούν:
, να βρεθούν: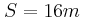 από τη στιγμή που άρχισε να επιβραδύνεται το τρακτέρ, από το ψηλότερο σημείο του μεγαλύτερου τροχού ξεκολλάει ένα κομμάτι λάσπης μάζας
από τη στιγμή που άρχισε να επιβραδύνεται το τρακτέρ, από το ψηλότερο σημείο του μεγαλύτερου τροχού ξεκολλάει ένα κομμάτι λάσπης μάζας 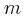 .
.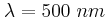 . Η ακτινοβολία προσπίπτει στη διαχωριστική επιφάνεια του σώματος με τον αέρα με γωνία πρόσπτωσης
. Η ακτινοβολία προσπίπτει στη διαχωριστική επιφάνεια του σώματος με τον αέρα με γωνία πρόσπτωσης 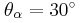 και ένα μέρος της διαθλάται. Η διαθλώμενη ακτινοβολία διαδίδεται με ταχύτητα κατά 40% μεγαλύτερη από την αντίστοιχη εντός του γυάλινου σώματος. Να υπολογίσετε:
και ένα μέρος της διαθλάται. Η διαθλώμενη ακτινοβολία διαδίδεται με ταχύτητα κατά 40% μεγαλύτερη από την αντίστοιχη εντός του γυάλινου σώματος. Να υπολογίσετε: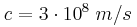 .
. .
.