Το αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς 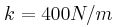 στερεώνεται ακλόνητα και στο δεξιό άκρο του προσδένεται σώμα Σ1 μάζας
στερεώνεται ακλόνητα και στο δεξιό άκρο του προσδένεται σώμα Σ1 μάζας 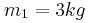 , το οποίο μπορεί να κινείται σε λείο οριζόντιο δάπεδο. Πάνω στο Σ1 τοποθετείται δεύτερο σώμα Σ2 μάζας
, το οποίο μπορεί να κινείται σε λείο οριζόντιο δάπεδο. Πάνω στο Σ1 τοποθετείται δεύτερο σώμα Σ2 μάζας 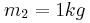 . Εκτοξεύουμε προς τα δεξιά το σύστημα από τη θέση ισορροπίας του, με ταχύτητα μέτρου
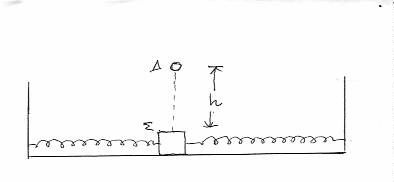
. Εκτοξεύουμε προς τα δεξιά το σύστημα από τη θέση ισορροπίας του, με ταχύτητα μέτρου 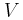 και παράλληλη με το οριζόντιο επίπεδο, όπως στο σχήμα, οπότε το σύστημα
εκτελεί γραμμική αρμονική ταλάντωση. Τα δυο σώματα διατηρούν την επαφή
στη διάρκεια της ταλάντωσης.
και παράλληλη με το οριζόντιο επίπεδο, όπως στο σχήμα, οπότε το σύστημα
εκτελεί γραμμική αρμονική ταλάντωση. Τα δυο σώματα διατηρούν την επαφή
στη διάρκεια της ταλάντωσης.

α) Να υπολογίσετε τη γωνιακή συχνότητα της ταλάντωσης καθώς και τις σταθερές ταλάντωσης
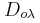
,
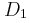
και
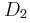
του συστήματος και των σωμάτων Σ
1 και Σ
2 αντίστοιχα.
β)
Να τοποθετήσετε το σύστημα σε μια τυχαία θέση της ταλάντωσής του, να
σχεδιάσετε και να περιγράψετε σε τρία κατάλληλα σχήματα τις δυνάμεις,
που δέχονται: i) το σύστημα Σ
1 – Σ
2, ii) το Σ
1 και iii) το Σ
2.
γ) Να παραστήσετε γραφικά την αλγεβρική τιμή της στατικής τριβής από το Σ
1 στο Σ
2 σε συνάρτηση με την απομάκρυνση
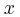
από τη θέση ισορροπίας του, για πλάτος ταλάντωσης
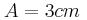
.
δ) Να υπολογίσετε τη μέγιστη τιμή της αρχικής ταχύτητας εκτόξευσης
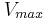
, του συστήματος των Σ
1, Σ
2 ώστε το σώμα Σ
2 να μην ολισθήσει πάνω στο σώμα Σ
1. Δίνεται η επιτάχυνση της βαρύτητας
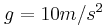
και ο συντελεστής στατικής τριβής μεταξύ των δύο σωμάτων Σ
1 και Σ
2 είναι
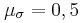
.
ΛΥΣΗ





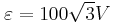 , η χωρητικότητα του πυκνωτή είναι C=10-6F, ο συντελεστής αυτεπαγωγής του ιδανικού πηνίου είναι L=10-2H και η αντίσταση του αντιστάτη είναι R=
, η χωρητικότητα του πυκνωτή είναι C=10-6F, ο συντελεστής αυτεπαγωγής του ιδανικού πηνίου είναι L=10-2H και η αντίσταση του αντιστάτη είναι R=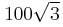 Ω. Ο διακόπτης Δ1 είναι κλειστός, ο Δ2 είναι ανοικτός και το πηνίο διαρρέεται από σταθερό ρεύμα. Τη χρονική στιγμή t=0 ο διακόπτης Δ1 ανοίγει και ταυτόχρονα κλείνει ο Δ2. Να βρείτε:
Ω. Ο διακόπτης Δ1 είναι κλειστός, ο Δ2 είναι ανοικτός και το πηνίο διαρρέεται από σταθερό ρεύμα. Τη χρονική στιγμή t=0 ο διακόπτης Δ1 ανοίγει και ταυτόχρονα κλείνει ο Δ2. Να βρείτε: 

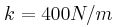 στερεώνεται ακλόνητα και στο δεξιό άκρο του προσδένεται σώμα Σ1 μάζας
στερεώνεται ακλόνητα και στο δεξιό άκρο του προσδένεται σώμα Σ1 μάζας 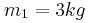 , το οποίο μπορεί να κινείται σε λείο οριζόντιο δάπεδο. Πάνω στο Σ1 τοποθετείται δεύτερο σώμα Σ2 μάζας
, το οποίο μπορεί να κινείται σε λείο οριζόντιο δάπεδο. Πάνω στο Σ1 τοποθετείται δεύτερο σώμα Σ2 μάζας 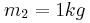 . Εκτοξεύουμε προς τα δεξιά το σύστημα από τη θέση ισορροπίας του, με ταχύτητα μέτρου
. Εκτοξεύουμε προς τα δεξιά το σύστημα από τη θέση ισορροπίας του, με ταχύτητα μέτρου 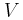 και παράλληλη με το οριζόντιο επίπεδο, όπως στο σχήμα, οπότε το σύστημα
εκτελεί γραμμική αρμονική ταλάντωση. Τα δυο σώματα διατηρούν την επαφή
στη διάρκεια της ταλάντωσης.
και παράλληλη με το οριζόντιο επίπεδο, όπως στο σχήμα, οπότε το σύστημα
εκτελεί γραμμική αρμονική ταλάντωση. Τα δυο σώματα διατηρούν την επαφή
στη διάρκεια της ταλάντωσης.
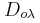 ,
, 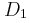 και
και 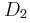 του συστήματος και των σωμάτων Σ1 και Σ2 αντίστοιχα.
του συστήματος και των σωμάτων Σ1 και Σ2 αντίστοιχα.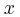 από τη θέση ισορροπίας του, για πλάτος ταλάντωσης
από τη θέση ισορροπίας του, για πλάτος ταλάντωσης 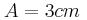 .
.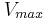 , του συστήματος των Σ1, Σ2 ώστε το σώμα Σ2 να μην ολισθήσει πάνω στο σώμα Σ1. Δίνεται η επιτάχυνση της βαρύτητας
, του συστήματος των Σ1, Σ2 ώστε το σώμα Σ2 να μην ολισθήσει πάνω στο σώμα Σ1. Δίνεται η επιτάχυνση της βαρύτητας 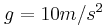 και ο συντελεστής στατικής τριβής μεταξύ των δύο σωμάτων Σ1 και Σ2 είναι
και ο συντελεστής στατικής τριβής μεταξύ των δύο σωμάτων Σ1 και Σ2 είναι 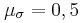 .
.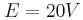 και εσωτερική αντίσταση
και εσωτερική αντίσταση 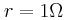 , ο αντιστάτης έχει αντίσταση
, ο αντιστάτης έχει αντίσταση 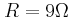 , ο πυκνωτής έχει χωρητικότητα
, ο πυκνωτής έχει χωρητικότητα 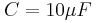 και το πηνίο έχει συντελεστή αυτεπαγωγής
και το πηνίο έχει συντελεστή αυτεπαγωγής 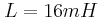 .
O μεταγωγός διακόπτης είναι αρχικά στη θέση (1) και το πηνίο διαρρέεται
από ηλεκτρικό ρεύμα σταθερής έντασης. Τη χρονική στιγμή
.
O μεταγωγός διακόπτης είναι αρχικά στη θέση (1) και το πηνίο διαρρέεται
από ηλεκτρικό ρεύμα σταθερής έντασης. Τη χρονική στιγμή 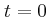 , μεταφέρουμε απότομα το διακόπτη στη θέση (2) χωρίς να δημιουργηθεί σπινθήρας, οπότε στο ιδανικό κύκλωμα
, μεταφέρουμε απότομα το διακόπτη στη θέση (2) χωρίς να δημιουργηθεί σπινθήρας, οπότε στο ιδανικό κύκλωμα 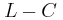 διεγείρεται αμείωτη ηλεκτρική ταλάντωση.
διεγείρεται αμείωτη ηλεκτρική ταλάντωση.
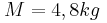 και ισορροπεί δεμένο στο κάτω άκρο κατακόρυφου μη εκτατού νήματος μήκους
και ισορροπεί δεμένο στο κάτω άκρο κατακόρυφου μη εκτατού νήματος μήκους 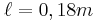 . Σώμα μάζας
. Σώμα μάζας 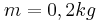 κινείται με ταχύτητα
κινείται με ταχύτητα 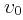 και συγκρούεται πλαστικά με το σώμα
και συγκρούεται πλαστικά με το σώμα 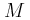 . Να υπολογίσετε:
. Να υπολογίσετε:
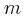 ώστε μετά την πλαστική τους κρούση, το συσσωμάτωμα να διαγράψει μία πλήρη κυκλική τροχιά (να κάνει ανακύκλωση).
ώστε μετά την πλαστική τους κρούση, το συσσωμάτωμα να διαγράψει μία πλήρη κυκλική τροχιά (να κάνει ανακύκλωση).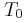 του νήματος πριν την κρούση.
του νήματος πριν την κρούση.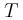 του νήματος αμέσως μετά την κρούση. Δίνεται η επιτάχυνση βαρύτητας
του νήματος αμέσως μετά την κρούση. Δίνεται η επιτάχυνση βαρύτητας 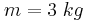 και ακτίνας
και ακτίνας 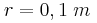 , μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που περνάει από το κέντρο της Ο και είναι κάθετος σε αυτήν. Στο αυλάκι της τροχαλίας περνά νήμα που από το ένα άκρο του κρέμεται σώμα
, μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που περνάει από το κέντρο της Ο και είναι κάθετος σε αυτήν. Στο αυλάκι της τροχαλίας περνά νήμα που από το ένα άκρο του κρέμεται σώμα 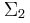 μάζας
μάζας 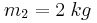 και στο άλλο άκρο του είναι δεμένος ένας κατακόρυφος τροχός
και στο άλλο άκρο του είναι δεμένος ένας κατακόρυφος τροχός 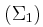 που έχει μάζα
που έχει μάζα 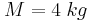 και ακτίνα
και ακτίνα 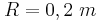 .
.
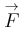 ώστε το σύστημα που εικονίζεται στο σχήμα να παραμείνει ακίνητο.
ώστε το σύστημα που εικονίζεται στο σχήμα να παραμείνει ακίνητο.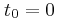 που το σύστημα του σχήματος είναι ακίνητο, αυξάνουμε τη δύναμη ακαριαία έτσι ώστε να γίνει
που το σύστημα του σχήματος είναι ακίνητο, αυξάνουμε τη δύναμη ακαριαία έτσι ώστε να γίνει 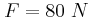 .
.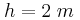 , να υπολογίσετε:
, να υπολογίσετε: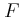 που μετατράπηκε σε κινητική ενέργεια του τροχού
που μετατράπηκε σε κινητική ενέργεια του τροχού 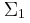 κατά τη μετατόπιση του σώματος
κατά τη μετατόπιση του σώματος 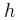 .
.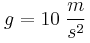 , η ροπή αδράνειας της τροχαλίας ως προς τον άξονα περιστροφής της
, η ροπή αδράνειας της τροχαλίας ως προς τον άξονα περιστροφής της 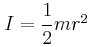 και του σώματος
και του σώματος 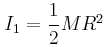 .
.