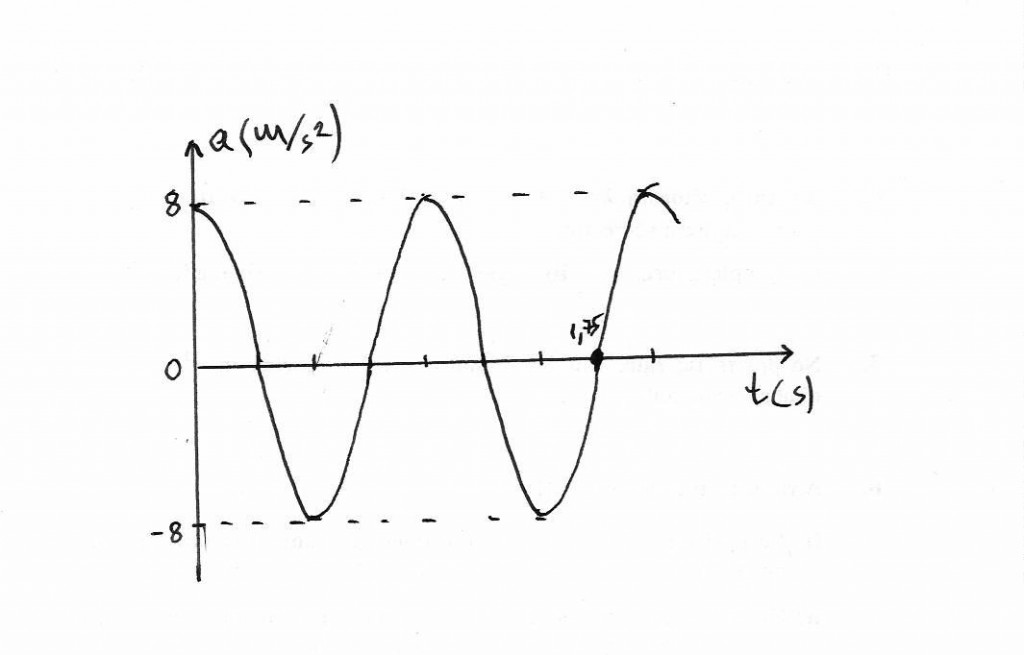
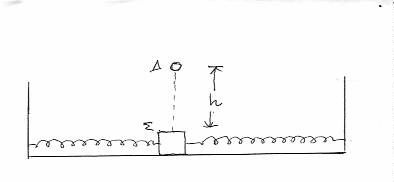
Μια οριζόντια πλατφόρμα εκτελεί
α.α.τ. σε οριζόντια διεύθυνση, ενώ πάνω της είναι τοποθετημένο ένα σώμα.
Η συχνότητα ταλάντωσης του συστήματος είναι f και ο συντελεστής τριβής
ανάμεσα στό σώμα και στην πλατφόρμα είναι μ. Για ποιες τιμές του
πλάτους της ταλάντωσης το σώμα δεν ολισθαίνει πάνω στην πλατφόρμα;
Δίνεται η g.
Λύση
Λύση