ΘΕΡΜΙΚΗ ΜΗΧΑΝΗ με συχνότητα 50Hz

Μια θερμική μηχανή απορροφά θερμότητα από χώρο θερμοκρασίας 400Κ και αποβάλλει το πλεόνασμα της θερμότητας σε χώρο θερμοκρασίας 300Κ. Η θερμική αυτή μηχανή αποδίδει μηχανική ενέργεια 400Joule ανά κύκλο και αποβάλλει θερμότητα στη δεξαμενή χαμηλής θερμοκρασίας 1600Joule ανά κύκλο. Αν η συχνότητα λειτουργίας της μηχανής είναι f=50Hz

Α) Ποιος ο συντελεστής απόδοσης της μηχανής.

Β) Ποια η ισχύς της μηχανής.

Γ) Ποια η προσφερόμενη ανά sec θερμότητα στη μηχανή

Δ) Πόση θερμότητα αποβάλλει στην ψυχρή δεξαμενή η μηχανή σε μία ώρα .

Ε).Ποια η μέγιστη δυνατή απόδοση της ανωτέρω μηχανής. Με ποιόν θερμοδυναμικό κύκλο μπορεί να πραγματοποιηθεί η μέγιστη δυνατή απόδοση της μηχανής. Να σχεδιασθεί ο κύκλος αυτός σε διάγραμμα P-V.

Σώμα συναντά πλάγιο ελατήριο α.α.τ. (Από τις ασκήσεις του Υ.Παι.Θ.)

Η μια άκρη ιδανικού ελατηρίου σταθεράς k=100N/m είναι στερεωμένη στο πάνω μέρος του πλάγιου επιπέδου γωνίας φ=30ο, όπως στο σχήμα. Από ένα σημείο του πλάγιου επιπέδου που απέχει s=0,25m από το ελεύθερο άκρο του ελατηρίου, εκτοξεύεται με αρχική ταχύτητα υο=2m/s, κατά μήκος του άξονα του ελατηρίου προς τα πάνω ένα σώμα Σ μάζας m=2kg. Όταν το σώμα ακουμπήσει στο ελατήριο, ενώνεται με αυτό και αρχίζει να εκτελεί αρμονική ταλάντωση.

α) Να βρείτε την ταχύτητα του σώματος τη στιγμή που έρχεται σε επαφή με το ελατήριο.
β) Να βρείτε τη μέγιστη ταχύτητα του σώματος.
γ) Να γράψετε τη συνάρτηση της απομάκρυνσης της ταλάντωσης σε σχέση με το χρόνο, θεωρώντας t=0 τη στιγμή της ένωσης του σώματος με το ελατήριο και τα θετικά προς τα πάνω.
δ) Να βρείτε το ρυθμό μεταβολής κινητικής ενέργειας του σώματος τη στιγμή που διέρχεται από το σημείο εκτόξευσης για δεύτερη φορά.
Δίνεται g=10m/s²
ΛΥΣΗ

Ηλεκτρική ταλάντωση (Από τις ασκήσεις του Υ.Παι.Θ.)

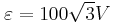Στο κύκλωμα του διπλανού σχήματος, η ΗΕΔ της ιδανικής πηγής είναι , η χωρητικότητα του πυκνωτή είναι C=10-6F, ο συντελεστής αυτεπαγωγής του ιδανικού πηνίου είναι L=10-2H και η αντίσταση του αντιστάτη είναι R=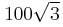Ω. Ο διακόπτης Δ1 είναι κλειστός, ο Δ2 είναι ανοικτός και το πηνίο διαρρέεται από σταθερό ρεύμα. Τη χρονική στιγμή t=0 ο διακόπτης Δ1 ανοίγει και ταυτόχρονα κλείνει ο Δ2. Να βρείτε:

α. την ηλεκτρική ενέργεια του πυκνωτή και τη μαγνητική ενέργεια του πηνίου όταν το πηνίο διαρρέεται από σταθερό ρεύμα.
β. μετά τη χρονική στιγμή t=0 , το μέγιστο φορτίο και τη μέγιστη ένταση του ηλεκτρικού ρεύματος του κυκλώματος LC.
γ. μετά τη χρονική στιγμή t=0 , τις εξισώσεις του φορτίου του πάνω οπλισμού του πυκνωτή και της έντασης του ρεύματος που διαρρέει το πηνίο στο κύκλωμα L-C σε συνάρτηση με το χρόνο.
δ. τη χρονική στιγμή t=0

1. το ρυθμό μεταβολής της έντασης του ρεύματος στο κύκλωμα.
2. το ρυθμό μεταβολής της ενέργειας του ηλεκτρικού πεδίου του πυκνωτή.

Θεωρείστε ότι κατά το άνοιγμα του Δ₁ και κλείσιμο του Δ₂ δεν έχουμε απώλεια ενέργειας στο κύκλωμα.
ΛΥΣΗ

Μεταβλητή δύναμη και α.α.τ. (Από τις ασκήσεις του Υ.Παι.Θ.)

Ένα σώμα μάζας m=2kg κινείται χωρίς τριβές σε λείο οριζόντιο επίπεδο με ταχύτητα μέτρου  . Τη χρονική στιγμή t=0 δέχεται την επίδραση οριζόντιας δύναμης, ίδιας φοράς με την ταχύτητα, της οποίας το μέτρο μεταβάλλεται σύμφωνα με τη σχέση α) Αφού βρείτε τη θέση ισορροπίας του σώματος, να αποδείξετε ότι αυτό θα εκτελέσει απλή αρμονική ταλάντωση. β) Να βρείτε το πλάτος της ταλάντωσης. γ) Να γράψετε την εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο και να βρείτε τη χρονική στιγμή που το σώμα θα σταματήσει για πρώτη φορά. δ) Nα βρείτε το ρυθμό μεταβολής της δυναμικής ενέργειας του σώματος τη στιγμή που το σώμα διέρχεται από τη θέση x2=+0,25m για πρώτη φορά. ΛΥΣΗ

Α.Α.Τ. Συστήματος σωμάτων (Από τις ασκήσεις του Υ.Παι.Θ.)

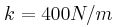Το αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς στερεώνεται ακλόνητα και στο δεξιό άκρο του προσδένεται σώμα Σ₁ μάζας 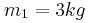, το οποίο μπορεί να κινείται σε λείο οριζόντιο δάπεδο. Πάνω στο Σ₁ τοποθετείται δεύτερο σώμα Σ₂ μάζας 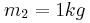. Εκτοξεύουμε προς τα δεξιά το σύστημα από τη θέση ισορροπίας του, με ταχύτητα μέτρου 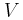και παράλληλη με το οριζόντιο επίπεδο, όπως στο σχήμα, οπότε το σύστημα εκτελεί γραμμική αρμονική ταλάντωση. Τα δυο σώματα διατηρούν την επαφή στη διάρκεια της ταλάντωσης.

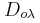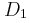α) Να υπολογίσετε τη γωνιακή συχνότητα της ταλάντωσης καθώς και τις σταθερές ταλάντωσης , και 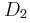του συστήματος και των σωμάτων Σ₁ και Σ₂ αντίστοιχα.
β) Να τοποθετήσετε το σύστημα σε μια τυχαία θέση της ταλάντωσής του, να σχεδιάσετε και να περιγράψετε σε τρία κατάλληλα σχήματα τις δυνάμεις, που δέχονται: i) το σύστημα Σ₁ – Σ₂, ii) το Σ₁ και iii) το Σ₂.
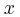γ) Να παραστήσετε γραφικά την αλγεβρική τιμή της στατικής τριβής από το Σ₁ στο Σ₂ σε συνάρτηση με την απομάκρυνση από τη θέση ισορροπίας του, για πλάτος ταλάντωσης .
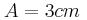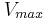δ) Να υπολογίσετε τη μέγιστη τιμή της αρχικής ταχύτητας εκτόξευσης , του συστήματος των Σ₁, Σ₂ ώστε το σώμα Σ₂ να μην ολισθήσει πάνω στο σώμα Σ₁. Δίνεται η επιτάχυνση της βαρύτητας 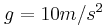και ο συντελεστής στατικής τριβής μεταξύ των δύο σωμάτων Σ₁ και Σ₂ είναι .
ΛΥΣΗ

ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ (Από τις ασκήσεις του Υ.Παι.Θ.)

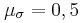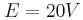Στο κύκλωμα του παρακάτω σχήματος η ηλεκτρική πηγή έχει ΗΕΔ και εσωτερική αντίσταση 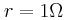, ο αντιστάτης έχει αντίσταση 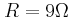, ο πυκνωτής έχει χωρητικότητα 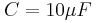και το πηνίο έχει συντελεστή αυτεπαγωγής 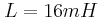. O μεταγωγός διακόπτης είναι αρχικά στη θέση (1) και το πηνίο διαρρέεται από ηλεκτρικό ρεύμα σταθερής έντασης. Τη χρονική στιγμή 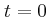, μεταφέρουμε απότομα το διακόπτη στη θέση (2) χωρίς να δημιουργηθεί σπινθήρας, οπότε στο ιδανικό κύκλωμα 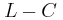διεγείρεται αμείωτη ηλεκτρική ταλάντωση.

α) Να βρείτε τη σταθερή ένταση του ρεύματος που διαρρέει το πηνίο καθώς και την αποθηκευμένη ενέργεια μαγνητικού πεδίου όταν ο διακόπτης βρίσκεται στη θέση (1).
β) Ποιος οπλισμός του πυκνωτή θα φορτιστεί πρώτος θετικά και γιατί; Ποιά χρονική στιγμή ο οπλισμός Δ του πυκνωτή θα αποκτήσει για πρώτη φορά μέγιστο φορτίο με αρνητική πολικότητα; Ποιά χρονική στιγμή το πηνίο για πρώτη φορά θα διαρρέεται από ρεύμα μέγιστης τιμής και φοράς από το Β προς το Α;
γ) Να γράψετε τις εξισώσεις που περιγράφουν πως μεταβάλλονται σε σχέση με το χρόνο στο S.I. το φορτίο του οπλισμού Δ του πυκνωτή και η ένταση του ρεύματος.
δ) Να βρείτε το μέτρο του ρυθμού μεταβολής της έντασης του ρεύματος τη στιγμή που η ένταση του ρεύματος στο κύκλωμα είναι μηδέν.
ΛΥΣΗ