Τρίτη 31 Δεκεμβρίου 2013
Δευτέρα 30 Δεκεμβρίου 2013
ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ
2013 12-30 ασκησεις για επαναληψη στην κυκλικη κινηση from nmandoulidis
Οι ασκήσεις είναι επιλεγμένες από το διαδίκτυο και κυρίως από την ιστοσελίδα ylikonet.gr
Μπορείτε να κατεβάσετε το αρχείο και από εδώ
Οι ασκήσεις είναι επιλεγμένες από το διαδίκτυο και κυρίως από την ιστοσελίδα ylikonet.gr
Μπορείτε να κατεβάσετε το αρχείο και από εδώ
Σάββατο 21 Δεκεμβρίου 2013
Παρασκευή 20 Δεκεμβρίου 2013
ΣΤΑΣΙΜΟ ΚΥΜΑ1 (απο τις ασκήσεις του Υ.ΠΑΙ.Θ.)
Οριζόντια ελαστική χορδή μήκους 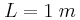 έχει το δεξί άκρο της Α
έχει το δεξί άκρο της Α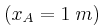 στερεωμένο σε ακλόνητο εμπόδιο. Το αριστερό άκρο Ο
στερεωμένο σε ακλόνητο εμπόδιο. Το αριστερό άκρο Ο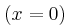 είναι ελεύθερο να κινηθεί. Στη χορδή έχει δημιουργηθεί στάσιμο κύμα, με το Ο να είναι κοιλία, η οποία ταλαντώνεται με πλάτος
είναι ελεύθερο να κινηθεί. Στη χορδή έχει δημιουργηθεί στάσιμο κύμα, με το Ο να είναι κοιλία, η οποία ταλαντώνεται με πλάτος 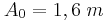 . Η μέγιστη ταχύτητα ταλάντωσης του Ο ισούται με
. Η μέγιστη ταχύτητα ταλάντωσης του Ο ισούται με 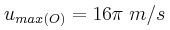 , ενώ μεταξύ των Ο και Α εμφανίζονται δύο δεσμοί.
, ενώ μεταξύ των Ο και Α εμφανίζονται δύο δεσμοί.
α) Να υπολογίσετε το μήκος κύματος των κυμάτων των οποίων η συμβολή παρήγαγε το στάσιμο.
β) Να γράψετε την εξίσωση του στάσιμου κύματος.
γ) Να σχεδιάσετε το στιγμιότυπο της χορδής τη χρονική στιγμή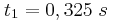 .
.
δ) Να υπολογίσετε την απομάκρυνση του υλικού σημείου Β(xΒ=0,9m) τη στιγμή που το υλικό σημείο Ο βρίσκεται σε ακραία αρνητική απομάκρυνση.
Λύση
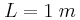 έχει το δεξί άκρο της Α
έχει το δεξί άκρο της Α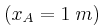 στερεωμένο σε ακλόνητο εμπόδιο. Το αριστερό άκρο Ο
στερεωμένο σε ακλόνητο εμπόδιο. Το αριστερό άκρο Ο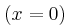 είναι ελεύθερο να κινηθεί. Στη χορδή έχει δημιουργηθεί στάσιμο κύμα, με το Ο να είναι κοιλία, η οποία ταλαντώνεται με πλάτος
είναι ελεύθερο να κινηθεί. Στη χορδή έχει δημιουργηθεί στάσιμο κύμα, με το Ο να είναι κοιλία, η οποία ταλαντώνεται με πλάτος 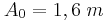 . Η μέγιστη ταχύτητα ταλάντωσης του Ο ισούται με
. Η μέγιστη ταχύτητα ταλάντωσης του Ο ισούται με 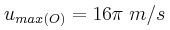 , ενώ μεταξύ των Ο και Α εμφανίζονται δύο δεσμοί.
, ενώ μεταξύ των Ο και Α εμφανίζονται δύο δεσμοί.α) Να υπολογίσετε το μήκος κύματος των κυμάτων των οποίων η συμβολή παρήγαγε το στάσιμο.
β) Να γράψετε την εξίσωση του στάσιμου κύματος.
γ) Να σχεδιάσετε το στιγμιότυπο της χορδής τη χρονική στιγμή
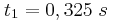 .
.δ) Να υπολογίσετε την απομάκρυνση του υλικού σημείου Β(xΒ=0,9m) τη στιγμή που το υλικό σημείο Ο βρίσκεται σε ακραία αρνητική απομάκρυνση.
Λύση
Τρίτη 17 Δεκεμβρίου 2013
ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ (απο τις ασκήσεις του Υ.ΠΑΙ.Θ.)
Δύο σύγχρονες πηγές 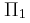 και
και 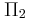 βρίσκονται στα σημεία Α και Β αντίστοιχα, της ελαστικής επιφάνειας ενός υγρού και απέχουν κατά
βρίσκονται στα σημεία Α και Β αντίστοιχα, της ελαστικής επιφάνειας ενός υγρού και απέχουν κατά 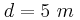 . Οι πηγές ξεκινούν τη χρονική στιγμή t = 0 να ταλαντώνονται κάθετα στην επιφάνεια του υγρού χωρίς αρχική φάση με συχνότητα
. Οι πηγές ξεκινούν τη χρονική στιγμή t = 0 να ταλαντώνονται κάθετα στην επιφάνεια του υγρού χωρίς αρχική φάση με συχνότητα 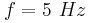 και ίδιο πλάτος δημιουργώντας κύματα, τα οποία συμβάλλουν στην επιφάνεια του υγρού. Σημείο (Σ) απέχει κατά
και ίδιο πλάτος δημιουργώντας κύματα, τα οποία συμβάλλουν στην επιφάνεια του υγρού. Σημείο (Σ) απέχει κατά 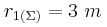 από την πηγή
από την πηγή 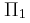 και κατά
και κατά 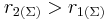 από την πηγή
από την πηγή 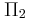 . Μετά τη συμβολή των κυμάτων σε αυτό, το (Σ) ταλαντώνεται σύμφωνα με την εξίσωση:
. Μετά τη συμβολή των κυμάτων σε αυτό, το (Σ) ταλαντώνεται σύμφωνα με την εξίσωση: 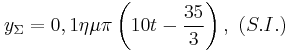 .
.
Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι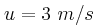 .
.
α) Να υπολογίσετε την απόσταση του (Σ) από την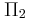 .
.
β) Να υπολογίσετε το πλήθος των σημείων ενίσχυσης που βρίσκονται πάνω στο τμήμα ΑΒ.
γ) Να προσδιορίσετε τη θέση του σημείου (Κ) το οποίο βρίσκεται επί του ΑΒ και ανήκει στην ίδια υπερβολή με το (Σ).
δ) Να γράψετε την εξίσωση απομάκρυνσης του σημείου (Κ) σε συνάρτηση με το χρόνο.
Λύση
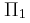 και
και 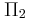 βρίσκονται στα σημεία Α και Β αντίστοιχα, της ελαστικής επιφάνειας ενός υγρού και απέχουν κατά
βρίσκονται στα σημεία Α και Β αντίστοιχα, της ελαστικής επιφάνειας ενός υγρού και απέχουν κατά 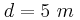 . Οι πηγές ξεκινούν τη χρονική στιγμή t = 0 να ταλαντώνονται κάθετα στην επιφάνεια του υγρού χωρίς αρχική φάση με συχνότητα
. Οι πηγές ξεκινούν τη χρονική στιγμή t = 0 να ταλαντώνονται κάθετα στην επιφάνεια του υγρού χωρίς αρχική φάση με συχνότητα 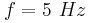 και ίδιο πλάτος δημιουργώντας κύματα, τα οποία συμβάλλουν στην επιφάνεια του υγρού. Σημείο (Σ) απέχει κατά
και ίδιο πλάτος δημιουργώντας κύματα, τα οποία συμβάλλουν στην επιφάνεια του υγρού. Σημείο (Σ) απέχει κατά 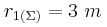 από την πηγή
από την πηγή 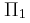 και κατά
και κατά 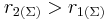 από την πηγή
από την πηγή 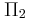 . Μετά τη συμβολή των κυμάτων σε αυτό, το (Σ) ταλαντώνεται σύμφωνα με την εξίσωση:
. Μετά τη συμβολή των κυμάτων σε αυτό, το (Σ) ταλαντώνεται σύμφωνα με την εξίσωση: 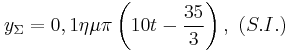 .
.Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι
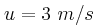 .
.α) Να υπολογίσετε την απόσταση του (Σ) από την
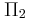 .
.β) Να υπολογίσετε το πλήθος των σημείων ενίσχυσης που βρίσκονται πάνω στο τμήμα ΑΒ.
γ) Να προσδιορίσετε τη θέση του σημείου (Κ) το οποίο βρίσκεται επί του ΑΒ και ανήκει στην ίδια υπερβολή με το (Σ).
δ) Να γράψετε την εξίσωση απομάκρυνσης του σημείου (Κ) σε συνάρτηση με το χρόνο.
Λύση
Δευτέρα 9 Δεκεμβρίου 2013
Παρασκευή 6 Δεκεμβρίου 2013
ΣΤΑΣΙΜΟ ΚΥΜΑ (απο τις ασκήσεις του Υ.ΠΑΙ.Θ.)
Δύο εγκάρσια αρμονικά κύματα με εξισώσεις 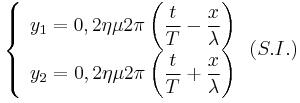 διαδίδονται με αντίθετες κατευθύνσεις σε γραμμικό ελαστικό μέσο το
οποίο ταυτίζεται με τον οριζόντιο άξονα x΄Οx. Τα κύματα συμβάλλουν και
δημιουργούν στάσιμο κύμα το οποίο στη θέση
διαδίδονται με αντίθετες κατευθύνσεις σε γραμμικό ελαστικό μέσο το
οποίο ταυτίζεται με τον οριζόντιο άξονα x΄Οx. Τα κύματα συμβάλλουν και
δημιουργούν στάσιμο κύμα το οποίο στη θέση 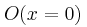 εμφανίζει κοιλία. Στο σημείο Α
εμφανίζει κοιλία. Στο σημείο Α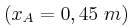 είναι ο πέμπτος δεσμός του θετικού ημιάξονα. Το σημείο Β
είναι ο πέμπτος δεσμός του θετικού ημιάξονα. Το σημείο Β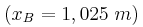 διέρχεται από τη θέση ισορροπίας του ανά
διέρχεται από τη θέση ισορροπίας του ανά 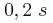 .
.
α) Να υπολογίσετε την ταχύτητα διάδοσης των κυμάτων.
β) Να γράψετε την εξίσωση του στάσιμου κύματος.
γ) Να υπολογίσετε την απομάκρυνση του σημείου Γ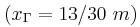 τη χρονική στιγμή που το σημείο Δ
τη χρονική στιγμή που το σημείο Δ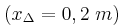 βρίσκεται σε ακραία θετική απομάκρυνση.
βρίσκεται σε ακραία θετική απομάκρυνση.
δ) Να σχεδιάσετε το στιγμιότυπο του τμήματος ΑΒ της χορδής τη χρονική στιγμή που η απομάκρυνση του Ο ισούται με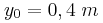 .
.
κατεβάστε τη λύση
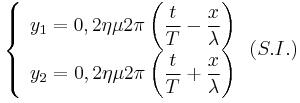 διαδίδονται με αντίθετες κατευθύνσεις σε γραμμικό ελαστικό μέσο το
οποίο ταυτίζεται με τον οριζόντιο άξονα x΄Οx. Τα κύματα συμβάλλουν και
δημιουργούν στάσιμο κύμα το οποίο στη θέση
διαδίδονται με αντίθετες κατευθύνσεις σε γραμμικό ελαστικό μέσο το
οποίο ταυτίζεται με τον οριζόντιο άξονα x΄Οx. Τα κύματα συμβάλλουν και
δημιουργούν στάσιμο κύμα το οποίο στη θέση 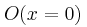 εμφανίζει κοιλία. Στο σημείο Α
εμφανίζει κοιλία. Στο σημείο Α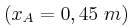 είναι ο πέμπτος δεσμός του θετικού ημιάξονα. Το σημείο Β
είναι ο πέμπτος δεσμός του θετικού ημιάξονα. Το σημείο Β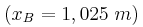 διέρχεται από τη θέση ισορροπίας του ανά
διέρχεται από τη θέση ισορροπίας του ανά 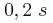 .
.α) Να υπολογίσετε την ταχύτητα διάδοσης των κυμάτων.
β) Να γράψετε την εξίσωση του στάσιμου κύματος.
γ) Να υπολογίσετε την απομάκρυνση του σημείου Γ
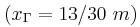 τη χρονική στιγμή που το σημείο Δ
τη χρονική στιγμή που το σημείο Δ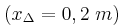 βρίσκεται σε ακραία θετική απομάκρυνση.
βρίσκεται σε ακραία θετική απομάκρυνση.δ) Να σχεδιάσετε το στιγμιότυπο του τμήματος ΑΒ της χορδής τη χρονική στιγμή που η απομάκρυνση του Ο ισούται με
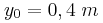 .
.κατεβάστε τη λύση
Κυριακή 1 Δεκεμβρίου 2013
ΣΥΜΒΟΛΗ2 ΚΥΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ (απο τις ασκήσεις του Υ.ΠΑΙ.Θ.)
Δύο σύγχρονες κυματικές πηγές 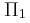 και
και 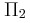 βρίσκονται στα σημεία Α και Β αντίστοιχα, της επιφάνειας ενός υγρού. Τη χρονική στιγμή
βρίσκονται στα σημεία Α και Β αντίστοιχα, της επιφάνειας ενός υγρού. Τη χρονική στιγμή 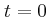 οι πηγές ξεκινούν να ταλαντώνονται κάθετα στην επιφάνεια του υγρού, με την απομάκρυνση τους να περιγράφεται από την εξίσωση
οι πηγές ξεκινούν να ταλαντώνονται κάθετα στην επιφάνεια του υγρού, με την απομάκρυνση τους να περιγράφεται από την εξίσωση 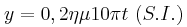 . Σημείο (Σ) της επιφάνειας απέχει κατά
. Σημείο (Σ) της επιφάνειας απέχει κατά 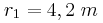 από την πηγή
από την πηγή 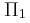 και κατά
και κατά 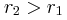 από την πηγή
από την πηγή 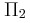 . Το (Σ) ξεκινά να ταλαντώνεται τη χρονική στιγμή
. Το (Σ) ξεκινά να ταλαντώνεται τη χρονική στιγμή 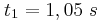 ενώ από τη χρονική στιγμή
ενώ από τη χρονική στιγμή 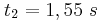 και έπειτα σταματά να κινείται.
και έπειτα σταματά να κινείται.
α) Να υπολογίσετε την ταχύτητα των κυμάτων και την απόσταση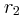 .
.
β) Να γράψετε την εξίσωση της απομάκρυνσης του (Σ) σε συνάρτηση με το χρόνο και της ταχύτητας ταλάντωσης του σε συνάρτηση με το χρόνο.
γ) Να κάνετε τη γραφική παράσταση της αλγεβρικής τιμής της επιτάχυνσης του (Σ) ως συνάρτηση του χρόνου σε κατάλληλα βαθμολογημένο σύστημα αξόνων.
δ) Να υπολογίσετε την ελάχιστη συχνότητα των κυμάτων που μπορούμε να προκαλέσουμε ώστε στο σημείο (Σ) να υπάρχει ενίσχυση των κυμάτων.
(Θεωρήστε ότι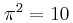 )
)
Λύση
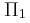 και
και 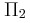 βρίσκονται στα σημεία Α και Β αντίστοιχα, της επιφάνειας ενός υγρού. Τη χρονική στιγμή
βρίσκονται στα σημεία Α και Β αντίστοιχα, της επιφάνειας ενός υγρού. Τη χρονική στιγμή 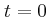 οι πηγές ξεκινούν να ταλαντώνονται κάθετα στην επιφάνεια του υγρού, με την απομάκρυνση τους να περιγράφεται από την εξίσωση
οι πηγές ξεκινούν να ταλαντώνονται κάθετα στην επιφάνεια του υγρού, με την απομάκρυνση τους να περιγράφεται από την εξίσωση 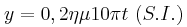 . Σημείο (Σ) της επιφάνειας απέχει κατά
. Σημείο (Σ) της επιφάνειας απέχει κατά 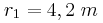 από την πηγή
από την πηγή 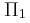 και κατά
και κατά 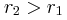 από την πηγή
από την πηγή 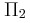 . Το (Σ) ξεκινά να ταλαντώνεται τη χρονική στιγμή
. Το (Σ) ξεκινά να ταλαντώνεται τη χρονική στιγμή 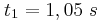 ενώ από τη χρονική στιγμή
ενώ από τη χρονική στιγμή 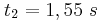 και έπειτα σταματά να κινείται.
και έπειτα σταματά να κινείται.α) Να υπολογίσετε την ταχύτητα των κυμάτων και την απόσταση
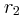 .
.β) Να γράψετε την εξίσωση της απομάκρυνσης του (Σ) σε συνάρτηση με το χρόνο και της ταχύτητας ταλάντωσης του σε συνάρτηση με το χρόνο.
γ) Να κάνετε τη γραφική παράσταση της αλγεβρικής τιμής της επιτάχυνσης του (Σ) ως συνάρτηση του χρόνου σε κατάλληλα βαθμολογημένο σύστημα αξόνων.
δ) Να υπολογίσετε την ελάχιστη συχνότητα των κυμάτων που μπορούμε να προκαλέσουμε ώστε στο σημείο (Σ) να υπάρχει ενίσχυση των κυμάτων.
(Θεωρήστε ότι
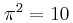 )
)Λύση
Πέμπτη 28 Νοεμβρίου 2013
ΣΥΜΒΟΛΗ1 ΚΥΜΑΤΩΝ Γ ΛΥΚΕΙΟΥ (απο τις ασκήσεις του Υ.ΠΑΙ.Θ.)
Δύο σύγχρονες κυματικές πηγές 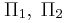 βρίσκονται στα σημεία Α και Β αντίστοιχα της επιφάνειας ενός υγρού. Οι πηγές απέχουν μεταξύ τους κατά
βρίσκονται στα σημεία Α και Β αντίστοιχα της επιφάνειας ενός υγρού. Οι πηγές απέχουν μεταξύ τους κατά 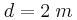 και ταλαντώνονται κάθετα στην επιφάνεια του υγρού, σύμφωνα με την
και ταλαντώνονται κάθετα στην επιφάνεια του υγρού, σύμφωνα με την 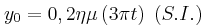 . Τα παραγόμενα κύματα διαδίδονται με ταχύτητα
. Τα παραγόμενα κύματα διαδίδονται με ταχύτητα 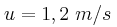 . Σημείο (Γ) της επιφάνειας του υγρού απέχει απόσταση
. Σημείο (Γ) της επιφάνειας του υγρού απέχει απόσταση 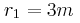 από την
από την 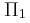 και
και 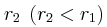 από την
από την 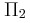 . Στο σημείο (Γ) τα κύματα φτάνουν με χρονική διαφορά
. Στο σημείο (Γ) τα κύματα φτάνουν με χρονική διαφορά 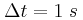 .
.
α) Να υπολογίσετε την απόσταση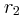 .
.
β) Να εξετάσετε αν το σημείο (Γ) είναι σημείο ενίσχυσης ή απόσβεσης.
γ) Να γράψετε την εξίσωση της απομάκρυνσης του σημείου (Γ) σε σχέση με το χρόνο και να σχεδιάσετε την αντίστοιχη γραφική παράσταση σε κατάλληλα βαθμολογημένο σύστημα αξόνων.
δ) Να υπολογίσετε το πλήθος των σημείων ενίσχυσης που βρίσκονται πάνω στο ευθύγραμμο τμήμα ΑΒ.
ε) Αν (Δ) σημείο του τμήματος ΑΒ, το οποίο ανήκει στην ίδια υπερβολή ενίσχυσης ή απόσβεσης με το σημείο (Γ) και (Ζ) σημείο του ΑΒ το οποίο είναι το πλησιέστερο στην πηγή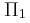 σημείο ενίσχυσης, να υπολογίσετε την απόσταση (ΔΖ).
σημείο ενίσχυσης, να υπολογίσετε την απόσταση (ΔΖ).
Κατεβάστε τη λύση.
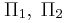 βρίσκονται στα σημεία Α και Β αντίστοιχα της επιφάνειας ενός υγρού. Οι πηγές απέχουν μεταξύ τους κατά
βρίσκονται στα σημεία Α και Β αντίστοιχα της επιφάνειας ενός υγρού. Οι πηγές απέχουν μεταξύ τους κατά 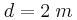 και ταλαντώνονται κάθετα στην επιφάνεια του υγρού, σύμφωνα με την
και ταλαντώνονται κάθετα στην επιφάνεια του υγρού, σύμφωνα με την 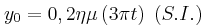 . Τα παραγόμενα κύματα διαδίδονται με ταχύτητα
. Τα παραγόμενα κύματα διαδίδονται με ταχύτητα 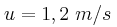 . Σημείο (Γ) της επιφάνειας του υγρού απέχει απόσταση
. Σημείο (Γ) της επιφάνειας του υγρού απέχει απόσταση 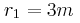 από την
από την 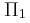 και
και 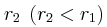 από την
από την 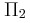 . Στο σημείο (Γ) τα κύματα φτάνουν με χρονική διαφορά
. Στο σημείο (Γ) τα κύματα φτάνουν με χρονική διαφορά 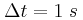 .
.α) Να υπολογίσετε την απόσταση
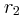 .
.β) Να εξετάσετε αν το σημείο (Γ) είναι σημείο ενίσχυσης ή απόσβεσης.
γ) Να γράψετε την εξίσωση της απομάκρυνσης του σημείου (Γ) σε σχέση με το χρόνο και να σχεδιάσετε την αντίστοιχη γραφική παράσταση σε κατάλληλα βαθμολογημένο σύστημα αξόνων.
δ) Να υπολογίσετε το πλήθος των σημείων ενίσχυσης που βρίσκονται πάνω στο ευθύγραμμο τμήμα ΑΒ.
ε) Αν (Δ) σημείο του τμήματος ΑΒ, το οποίο ανήκει στην ίδια υπερβολή ενίσχυσης ή απόσβεσης με το σημείο (Γ) και (Ζ) σημείο του ΑΒ το οποίο είναι το πλησιέστερο στην πηγή
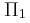 σημείο ενίσχυσης, να υπολογίσετε την απόσταση (ΔΖ).
σημείο ενίσχυσης, να υπολογίσετε την απόσταση (ΔΖ).Κατεβάστε τη λύση.
Τετάρτη 27 Νοεμβρίου 2013
Τρίτη 26 Νοεμβρίου 2013
ΑΣΚΗΣΕΙΣ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
7.
Φως μήκους κύματος λ0=525nm
στον αέρα, περνά μέσα από κρύσταλλο που
έχει δείκτη διάθλασης 1,5 και πάχος 10cm.
Α.
ποια είναι η ταχύτητα του φωτός στον
κρύσταλλο
Β.
με πόσα μήκη κύματος του φωτός όταν
διαδίδεται στον κρύσταλλο ισοδυναμεί
το πάχος του κρυστάλλου
Γ.
ποια μεταβολή θα έχουμε στην ενέργεια
του κάθε φωτονίου κατά το πέρασμα του
από τον αέρα στον κρύσταλλο.
8.
Ο δείκτης διάθλασης του τετραχλωράνθρακα
είναι η=1,46. Yπολογίστε:
Α.
Την ταχύτητα διάδοσης του φωτός στον
τετραχλωράνθρακα
Β.
τον λόγο όπου λ0 το μήκος κύματος
μιας ακτινοβολίας στο κενό και λ1
το μήκος κύματος της ίδιας ακτινοβολίας
στον τετραχλωράνθρακα.
Γ.
τον λόγο όπου Ε0 η ενέργεια ενός
φωτονίου της ακτινοβολίας στο κενό και
Ε1 η ενέργεια ενός φωτονίου της
ίδιας ακτινοβολίας στον τετραχλωράνθρακα.
9.
Το μήκος κύματος μιας ακτινοβολίας
στο κενό είναι λ0=600nm. υπολογίστε:
Α.
τη συχνότητα της ακτινοβολίας
Β.
την ενέργεια κάθε φωτονίου της ακτινοβολίας
Γ.
τον αριθμό φωτονίων που χρειάζεται για
να ανεβάσουν τη θερμοκρασία 10g
νερού κατά 50C αν το
κάθε g νερού χρειάζεται
ενέργεια 4,2j για να αυξήσει
τη θερμοκρασία του κατά 10C.
10.
Φωτεινή πηγή Π εκπέμπει μια μονοχρωματική
ακτίνα με λο = 600nm .
Μεταξύ της πηγής και μιας οθόνης που
απέχει D = 3,64m
από αυτή , τοποθετείται γυάλινο πλακίδιο
,κάθετο στη διεύθυνση διάδοσης της
ακτίνας , το οποίο έχει πάχος d
= 4cm . Δίνεται ο δείκτης
διάθλασης του γυαλιού n
= 1.5
Να
υπολογιστούν :
Α)
το μήκος κύματος της ακτινοβολίας και
η ταχύτητά της , στο πλακίδιο
Β)
ο αριθμός των μηκών κύματος που
περιλαμβάνονται μεταξύ πηγής
και
οθόνης
Γ)
η χρονική καθυστέρηση που επιφέρει στην
ακτίνα η ύπαρξη του πλακιδίου.
Δευτέρα 18 Νοεμβρίου 2013
Μερικές ασκήσεις γιά κάποιους που πήραν την Φυσική ως μάθημα επιλογής στην Γ Λυκείου (θα έχουμε συνέχεια αν υπάρξει ενδιαφέρον)
ΦΩΣ – ΔΙΑΘΛΑΣΗ
Σε όλες τις ασκήσεις να θεωρηθεί οτι δίνονται: h= 6,63Χ10-34js και c0=3X108m/s.
1. Ποια
τιμή πρέπει να έχει ο δείκτης διάθλασης ενός οπτικού μέσου , ώστε στο
μέσο αυτό η ταχύτητα του φωτός να είναι μικρότερη κατά 10% από τη
ταχύτητα του φωτός στο κενό.
2. Μια μονοχρωματική ακτινοβολία έχει μήκος κύματος 630nm στο κενό , το
μήκος κύματος γίνεται 420nm όταν διαδίδεται σε γυαλί.Να βρεθεί:
α) O δείκτης διάθλασης του γυαλιού.
β) ταχύτητα διάδοσης της ακτινοβολίας στο γυαλί.
γ)Η συχνότητα της ακτινοβολίας .
3. Ο δείκτης διάθλασης του νερού για μια μονοχρωματική ακτινοβολία, με μήκος κύματος λν=400nm μέσα στο νερό είναι nν=14/10. Αν ο δείκτης διάθλασης ενός γυαλιού είναι για την παραπάνω ακτινοβολία nγ=16/10 να βρείτε το μήκος κύματος αυτής της ακτινοβολίας στο γυαλί.
4. Ένα laser μονοχρωματικής ακτινοβολίας με μήκος κύματος λ=600nm στον αέρα έχει ισχύ P=660KW. Να υπολογίσετε τον αριθμό των φωτονίων ανά δευτερόλεπτο που φεύγουν από το laser.
5.
Το μήκος κύματος, στο κενό, μιας μονοχρωματικής δέσμης φωτός είναι 500
nm. Αν η ίδια ακτινοβολία διαδοθεί μέσα σε διαφανές υλικό με δείκτη
διάθλασης n = 1,25, να βρείτε:
Α) το μήκος κύματός της και την ταχύτητα διάδοσής της στο διαφανές υλικό.
Β) τη συχνότητα της ακτινοβολίας στο κενό.
Γ) τον λόγο των περιόδων των ακτινοβολιών, στο κενό και στο διαφανές υλικό.Κυριακή 17 Νοεμβρίου 2013
ΚΡΟΥΣΗ ΚΑΙ ΣΥΣΣΩΜΑΤΩΜΑ Β ΛΥΚΕΙΟΥ
Ένα βλήμα μάζας m=0,1kg κινείται με ταχύτητα υ0=100m/s
και σφηνώνεται σε ακίνητο σώμα Σ μάζας Μ=1,9kg. Το συσσωμάτωμα κινείται
στο οριζόντιο επίπεδο και σταματά αφού μετατοπισθεί κατά x=10m.
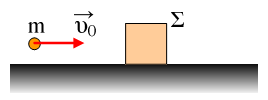
α) Ποια είναι η κοινή ταχύτητα του συσσωματώματος αμέσως μετά την κρούση;
β) Βρείτε την δύναμη της τριβής που ασκήθηκε στο συσσωμάτωμα κατά τη διάρκεια της κίνησής του.
γ) Πόσο χρόνο διαρκεί η κίνηση μετά την κρούση;
Δίνεται g=10m/s2.
(5m/s, 2,5Ν, 4s.)
Λύση
α) Ποια είναι η κοινή ταχύτητα του συσσωματώματος αμέσως μετά την κρούση;
β) Βρείτε την δύναμη της τριβής που ασκήθηκε στο συσσωμάτωμα κατά τη διάρκεια της κίνησής του.
γ) Πόσο χρόνο διαρκεί η κίνηση μετά την κρούση;
Δίνεται g=10m/s2.
(5m/s, 2,5Ν, 4s.)
Λύση
ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΤΗΣ ΦΑΣΗΣ ΤΩΝ ΣΗΜΕΙΩΝ ΜΙΑΣ ΟΜΟΓΕΝΟΥΣ ΕΛΑΣΤΙΚΗΣ ΧΟΡΔΗΣ (ψηφιακά εκπαιδευτικά βοηθήματα Υ.ΠΑΙ.Θ.)
Το σχήμα παρουσιάζει τη γραφική παράσταση  της φάσης των σημείων μιας ομογενούς ελαστικής χορδής, στην οποία διαδίδεται ένα εγκάρσιο αρμονικό κύμα, τη χρονική στιγμή
της φάσης των σημείων μιας ομογενούς ελαστικής χορδής, στην οποία διαδίδεται ένα εγκάρσιο αρμονικό κύμα, τη χρονική στιγμή 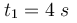 . Το πλάτος της ταλάντωσης των σημείων από τα οποία περνά το κύμα είναι
. Το πλάτος της ταλάντωσης των σημείων από τα οποία περνά το κύμα είναι 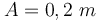 . Δύο σημεία Κ και Λ της χορδής βρίσκονται στις θέσεις
. Δύο σημεία Κ και Λ της χορδής βρίσκονται στις θέσεις  και
και 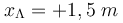 , αντίστοιχα. Για το σημείο της θέσης
, αντίστοιχα. Για το σημείο της θέσης 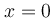 γνωρίζουμε ότι τη χρονική στιγμή
γνωρίζουμε ότι τη χρονική στιγμή 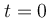 το σημείο αυτό διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα.
το σημείο αυτό διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα.

α) Να γραφεί η εξίσωση του κύματος.
β) Να γραφεί η εξίσωση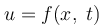 της ταχύτητας ταλάντωσης των σημείων του ελαστικού μέσου.
της ταχύτητας ταλάντωσης των σημείων του ελαστικού μέσου.
γ) να βρεθούν οι χρονικές στιγμές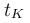 και
και 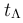 , στις οποίες τα σημεία Κ και Λ ξεκινούν ταλάντωση.
, στις οποίες τα σημεία Κ και Λ ξεκινούν ταλάντωση.
δ) Να υπολογιστεί η διαφορά φάσης μεταξύ των ταλαντώσεων των σημείων Κ και Λ την ίδια χρονική στιγμή.
ε) Να γίνει η γραφική παράσταση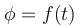 του σημείου Λ, μέχρι τη στιγμή που το σημείο Λ έχει εκτελέσει μία πλήρη ταλάντωση.
του σημείου Λ, μέχρι τη στιγμή που το σημείο Λ έχει εκτελέσει μία πλήρη ταλάντωση.
στ) Να γίνει η γραφική παράσταση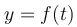 του σημείου Λ, μέχρι τη στιγμή που το σημείο Λ έχει εκτελέσει 2 πλήρεις ταλαντώσεις.
του σημείου Λ, μέχρι τη στιγμή που το σημείο Λ έχει εκτελέσει 2 πλήρεις ταλαντώσεις.
ζ) Να βρεθεί η φορά κίνησης του σημείου Λ, τη χρονική στιγμή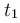 .
.
η) Να σχεδιαστεί το στιγμιότυπο του κύματος τη χρονική στιγμή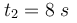 .
.
Κατεβάστε την Ασκηση και την Λύση της
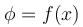 της φάσης των σημείων μιας ομογενούς ελαστικής χορδής, στην οποία διαδίδεται ένα εγκάρσιο αρμονικό κύμα, τη χρονική στιγμή
της φάσης των σημείων μιας ομογενούς ελαστικής χορδής, στην οποία διαδίδεται ένα εγκάρσιο αρμονικό κύμα, τη χρονική στιγμή 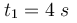 . Το πλάτος της ταλάντωσης των σημείων από τα οποία περνά το κύμα είναι
. Το πλάτος της ταλάντωσης των σημείων από τα οποία περνά το κύμα είναι 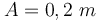 . Δύο σημεία Κ και Λ της χορδής βρίσκονται στις θέσεις
. Δύο σημεία Κ και Λ της χορδής βρίσκονται στις θέσεις  και
και 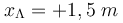 , αντίστοιχα. Για το σημείο της θέσης
, αντίστοιχα. Για το σημείο της θέσης 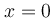 γνωρίζουμε ότι τη χρονική στιγμή
γνωρίζουμε ότι τη χρονική στιγμή 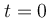 το σημείο αυτό διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα.
το σημείο αυτό διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα.
α) Να γραφεί η εξίσωση του κύματος.
β) Να γραφεί η εξίσωση
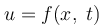 της ταχύτητας ταλάντωσης των σημείων του ελαστικού μέσου.
της ταχύτητας ταλάντωσης των σημείων του ελαστικού μέσου.γ) να βρεθούν οι χρονικές στιγμές
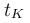 και
και 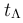 , στις οποίες τα σημεία Κ και Λ ξεκινούν ταλάντωση.
, στις οποίες τα σημεία Κ και Λ ξεκινούν ταλάντωση.δ) Να υπολογιστεί η διαφορά φάσης μεταξύ των ταλαντώσεων των σημείων Κ και Λ την ίδια χρονική στιγμή.
ε) Να γίνει η γραφική παράσταση
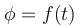 του σημείου Λ, μέχρι τη στιγμή που το σημείο Λ έχει εκτελέσει μία πλήρη ταλάντωση.
του σημείου Λ, μέχρι τη στιγμή που το σημείο Λ έχει εκτελέσει μία πλήρη ταλάντωση.στ) Να γίνει η γραφική παράσταση
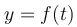 του σημείου Λ, μέχρι τη στιγμή που το σημείο Λ έχει εκτελέσει 2 πλήρεις ταλαντώσεις.
του σημείου Λ, μέχρι τη στιγμή που το σημείο Λ έχει εκτελέσει 2 πλήρεις ταλαντώσεις.ζ) Να βρεθεί η φορά κίνησης του σημείου Λ, τη χρονική στιγμή
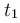 .
.η) Να σχεδιαστεί το στιγμιότυπο του κύματος τη χρονική στιγμή
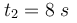 .
. Κατεβάστε την Ασκηση και την Λύση της
Εγγραφή σε:
Αναρτήσεις (Atom)