40. Ένα διαπασών παράγει ήχο συχνότητας 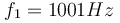 . Αν φέρουμε πολύ κοντά ένα δεύτερο διαπασών, περίπου ίδιο με το πρώτο, παράγεται και ένας δεύτερος ήχος συχνότητας
. Αν φέρουμε πολύ κοντά ένα δεύτερο διαπασών, περίπου ίδιο με το πρώτο, παράγεται και ένας δεύτερος ήχος συχνότητας 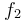 που είναι λίγο μικρότερη από την πρώτη. Ο σύνθετος ήχος που ακούει τότε ένας παρατηρητής έχει συχνότητα
που είναι λίγο μικρότερη από την πρώτη. Ο σύνθετος ήχος που ακούει τότε ένας παρατηρητής έχει συχνότητα 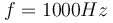 . Να υπολογισθεί:
. Να υπολογισθεί:
α) η συχνότητα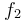 .
.
β) η συχνότητα μεταβολής του πλάτους της σύνθετης κίνησης.
γ) πόσες φορές μηδενίζεται η ένταση του ήχου που ακούει ο παρατηρητής σε χρόνο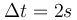 .
.
δ) Ένα μόριο του αέρα ταλαντώνεται εξαιτίας του ήχου που παράγουν τα διαπασών. Να υπολογισθεί πόσες φορές περνά από τη θέση ισορροπίας του σε χρόνο ίσο με τη περίοδο των διακροτημάτων.
α) η συχνότητα
β) η συχνότητα μεταβολής του πλάτους της σύνθετης κίνησης.
γ) πόσες φορές μηδενίζεται η ένταση του ήχου που ακούει ο παρατηρητής σε χρόνο
δ) Ένα μόριο του αέρα ταλαντώνεται εξαιτίας του ήχου που παράγουν τα διαπασών. Να υπολογισθεί πόσες φορές περνά από τη θέση ισορροπίας του σε χρόνο ίσο με τη περίοδο των διακροτημάτων.
[999Hz, 2Hz, 4, 1000]
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου