Α.Α.Τ. Συστήματος σωμάτων (Από τις ασκήσεις του Υ.Παι.Θ.)

Το αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς 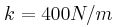στερεώνεται ακλόνητα και στο δεξιό άκρο του προσδένεται σώμα Σ₁ μάζας 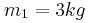, το οποίο μπορεί να κινείται σε λείο οριζόντιο δάπεδο. Πάνω στο Σ₁ τοποθετείται δεύτερο σώμα Σ₂ μάζας 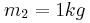. Εκτοξεύουμε προς τα δεξιά το σύστημα από τη θέση ισορροπίας του, με ταχύτητα μέτρου 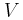και παράλληλη με το οριζόντιο επίπεδο, όπως στο σχήμα, οπότε το σύστημα εκτελεί γραμμική αρμονική ταλάντωση. Τα δυο σώματα διατηρούν την επαφή στη διάρκεια της ταλάντωσης.

α) Να υπολογίσετε τη γωνιακή συχνότητα της ταλάντωσης καθώς και τις σταθερές ταλάντωσης 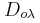, 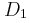και 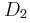του συστήματος και των σωμάτων Σ₁ και Σ₂ αντίστοιχα.
β) Να τοποθετήσετε το σύστημα σε μια τυχαία θέση της ταλάντωσής του, να σχεδιάσετε και να περιγράψετε σε τρία κατάλληλα σχήματα τις δυνάμεις, που δέχονται: i) το σύστημα Σ₁ – Σ₂, ii) το Σ₁ και iii) το Σ₂.
γ) Να παραστήσετε γραφικά την αλγεβρική τιμή της στατικής τριβής από το Σ₁ στο Σ₂ σε συνάρτηση με την απομάκρυνση 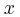από τη θέση ισορροπίας του, για πλάτος ταλάντωσης .
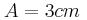δ) Να υπολογίσετε τη μέγιστη τιμή της αρχικής ταχύτητας εκτόξευσης 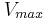, του συστήματος των Σ₁, Σ₂ ώστε το σώμα Σ₂ να μην ολισθήσει πάνω στο σώμα Σ₁. Δίνεται η επιτάχυνση της βαρύτητας 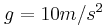και ο συντελεστής στατικής τριβής μεταξύ των δύο σωμάτων Σ₁ και Σ₂ είναι .
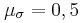ΛΥΣΗ