Η κυκλική περιστρεφόμενη πλατφόρμα της παιδικής χαράς της γειτονιάς μας έχει ακτίνα  , μάζα
, μάζα  και μπορεί να περιστρέφεται χωρίς τριβές γύρω από κατακόρυφο άξονα που περνά από το κέντρο της. Στο κέντρο της πλατφόρμας βρίσκεται ένα κορίτσι μάζας
και μπορεί να περιστρέφεται χωρίς τριβές γύρω από κατακόρυφο άξονα που περνά από το κέντρο της. Στο κέντρο της πλατφόρμας βρίσκεται ένα κορίτσι μάζας  και το σύστημα πλατφόρμα – κορίτσι περιστρέφεται με γωνιακή ταχύτητα
και το σύστημα πλατφόρμα – κορίτσι περιστρέφεται με γωνιακή ταχύτητα  . Κάποια στιγμή το κορίτσι αρχίζει να περπατά προς την περιφέρεια της πλατφόρμας. Να βρείτε:
. Κάποια στιγμή το κορίτσι αρχίζει να περπατά προς την περιφέρεια της πλατφόρμας. Να βρείτε:
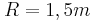 , μάζα
, μάζα 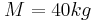 και μπορεί να περιστρέφεται χωρίς τριβές γύρω από κατακόρυφο άξονα που περνά από το κέντρο της. Στο κέντρο της πλατφόρμας βρίσκεται ένα κορίτσι μάζας
και μπορεί να περιστρέφεται χωρίς τριβές γύρω από κατακόρυφο άξονα που περνά από το κέντρο της. Στο κέντρο της πλατφόρμας βρίσκεται ένα κορίτσι μάζας 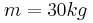 και το σύστημα πλατφόρμα – κορίτσι περιστρέφεται με γωνιακή ταχύτητα
και το σύστημα πλατφόρμα – κορίτσι περιστρέφεται με γωνιακή ταχύτητα 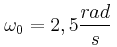 . Κάποια στιγμή το κορίτσι αρχίζει να περπατά προς την περιφέρεια της πλατφόρμας. Να βρείτε:
. Κάποια στιγμή το κορίτσι αρχίζει να περπατά προς την περιφέρεια της πλατφόρμας. Να βρείτε:
α) τη ροπή αδράνειας του συστήματος πλατφόρμα-κορίτσι όταν το κορίτσι βρίσκεται στην περιφέρεια της πλατφόρμας.
β) τη γωνιακή ταχύτητα του συστήματος, όταν το κορίτσι φτάσει στην περιφέρεια της πλατφόρμας.
γ) την κεντρομόλο δύναμη που δέχεται το κορίτσι όταν φτάσει στην περιφέρεια της πλατφόρμας.
δ) την ελάχιστη τιμή που πρέπει να έχει ο συντελεστής τριβής μεταξύ δαπέδου και παπουτσιών για να μπορεί το κορίτσι να περιστρέφεται χωρίς να κρατιέται όταν βρίσκεται στην περιφέρεια της πλατφόρμας.
Δίνεται η ροπή αδράνειας της πλατφόρμας ως προς άξονα που είναι κάθετος σε αυτήν και διέρχεται από το μέσον της, . Για τον υπολογισμό της ροπής αδράνειας το κορίτσι να θεωρηθεί υλικό σημείο.
. Για τον υπολογισμό της ροπής αδράνειας το κορίτσι να θεωρηθεί υλικό σημείο.
β) τη γωνιακή ταχύτητα του συστήματος, όταν το κορίτσι φτάσει στην περιφέρεια της πλατφόρμας.
γ) την κεντρομόλο δύναμη που δέχεται το κορίτσι όταν φτάσει στην περιφέρεια της πλατφόρμας.
δ) την ελάχιστη τιμή που πρέπει να έχει ο συντελεστής τριβής μεταξύ δαπέδου και παπουτσιών για να μπορεί το κορίτσι να περιστρέφεται χωρίς να κρατιέται όταν βρίσκεται στην περιφέρεια της πλατφόρμας.
Δίνεται η ροπή αδράνειας της πλατφόρμας ως προς άξονα που είναι κάθετος σε αυτήν και διέρχεται από το μέσον της,
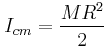 . Για τον υπολογισμό της ροπής αδράνειας το κορίτσι να θεωρηθεί υλικό σημείο.
. Για τον υπολογισμό της ροπής αδράνειας το κορίτσι να θεωρηθεί υλικό σημείο.
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου